Генетика популяцій. Матеріал для учнів 10 класу.

                             ЗАКОНОМІРНОСТІ РОЗПОДІЛУ АЛЕЛІВ У ПОПУЛЯЦІЇ

Яке значення має генетика популяцій?
ГЕНЕТИКА ПОПУЛЯЦІЙ — наука, що вивчає генетичну структуру природних популяцій, а також генетичні процеси, що в них відбуваються. Засновниками науки є Р. Фішер, Дж. Холдейн, С. Райт, С. С. Четвериков, С. М. Гершензон та ін. Основною метою досліджень популяційної генетики є пізнання законів, що пояснюють залежності між генотипами та фенотипами особин на популяційно-видовому рівні популяцій.
Генетика популяцій має значення для розвитку еволюційної теорії. Так, завдяки її досягненням встановлено, що елементарною одиницею еволюції є популяція, а не окрема особина, що природні популяції насичені різноманітними рецесивними мутаціями, які є «резервом спадкової мінливості» та ін. (іл. 115).

Іл. 115. Поширення Людини розумної з Африки по світу (шляхи міграції й кількість років тому)

Методи дослідження генетичного складу популяцій використовуються в антропології для вивчення історичного походження та становлення людини розумної.
Генетика популяції відіграє важливу роль в етології для досліджень поведінки організмів. Рівень генетичного поліморфізму вважається в популяційній генетиці важливим показником, від якого залежать еволюційна пластичність виду та його пристосованість до змін середовища. Як з'ясувалося, низький генетичний поліморфізм притаманний видам, у яких нечисленні, але великі й захищені нащадки, а високий — видам, у яких нащадки численні, дрібні й незахищені. Такий результат змушує по-новому оцінити еволюційну роль турботи про потомство.
Знання закономірностей популяційної генетики дають ключ для розуміння еволюції споріднених груп у систематиці, полегшують пошуки вихідного спадкового матеріалу в селекції та вивчення спадкових захворювань людини у медицині тощо.
Отже, дослідження генетики популяцій є актуальними й затребувані у багатьох галузях діяльності людини.
У чому суть закону генетичної рівноваги?
Математичну залежність між частотами алелів і генотипів в ідеальній популяції встановили одночасно у 1908 р. і незалежно один від одного видатний англійський математик Дж. Харді (1877—1947) і німецький лікар В. Вайнберг (1862—1937) (іл. 116). Ця закономірність відома як закон Харді — Вайнберга (закон генетичної рівноваги), який є основним законом генетики популяцій.

Іл. 116. Дж. Харді (ліворуч) і В. Вайнберг

Частоти алелей і генотипів у популяції залишатимуться сталими з покоління в покоління за наявності певних умов.
Рівняння Харді — Вайнберга:
p (А) + q (а) = 1 (для визначення генетичної структури популяцій за частотою алелей);
р² (АА) + 2pq (Аа) + q² (аа) = 1 (для визначення генетичної структури популяцій за частотою генотипів).
У популяційній генетиці частоту домінантного алеля А позначають через р, частоту рецесивного алеля а — через q. За умови, що А i a — єдині алелі гена, р + q = 1 (або 100%). Формула (р + q)²= р² + 2рq + q² = 1 (або 100 %) є алгебраїчним виразом закону Харді — Вайнберга для двох алелів, де р — частота домінантного алеля А; q — частота рецесивного алеля а; р² — частота домінантних гомозигот АА; 2pq — частота гетерозигот Аа; q² — частота рецесивних гомозигот аа (іл. 117).

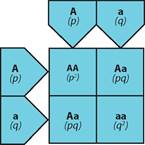
Іл. 117. Схема отримання алгебраїчного виразу закону Харді — Вайнберга

Популяція, в якій зберігається генетична рівновага, називається ідеальною популяцією. Умовами існування ідеальних популяцій є: 1) велика чисельність популяції; 2) вільне випадкове схрещування в популяції (панміксія); 3) відсутність мутацій; 4) відсутність добору за певною ознакою; 5) відсутність генного потоку, тобто міграцій генів із сусідніх популяцій. Якщо порушується хоча б одна умова, то генетична структура популяції змінюється.
У природі ідеальні популяції не трапляються, існують реальні популяції, в яких чисельність особин не буває нескінченно великою, вільне схрещування неабсолютне, відбуваються мутаційний процес, природний добір, міграції. Але це не зменшує цінності закону Харді — Вайнберга. Він визначає умови генетичної рівноваги популяції та умови, що її порушують.
Отже, закон Харді — Вайнберга дає змогу визначити генетичну структуру популяції та тенденції зміни генотипів особин у популяціях під дією умов середовища.
Яке значення закону гомологічних рядів спадкової мінливості?
Порівнюючи ознаки різних сортів культурних рослин і близьких до них диких видів, М. І. Вавилов (1887—1943) виявив багато спільних спадкових змін. Це допомогло йому сформулювати у 1920 р. закон гомологічних рядів спадкової мінливості.
Генетично близькі види та роди характеризуються подібними рядами спадкової мінливості з такою правильністю, що вивчивши ряд форм у межах одного виду чи роду, можна передбачити наявність форм із подібними поєднаннями ознак у межах близьких видів чи родів.
М. І. Вавилов зазначав, що гомологічні ряди часто виходять за межі родів і навіть родин. Короткопалість відмічено у представників багатьох рядів ссавців: у великої рогатої худоби, овець, собак, людини. Альбінізм поширений у всіх людських расах і спостерігається в усіх класів хребетних тварин.
Основою гомологічних рядів є подібність фенотипів, що виникає як результат взаємодії однакових генів у генотипах особин різних популяцій. Теоретичною основою гомології рядів спадкової мінливості у близьких таксономічних груп є уявлення про єдність їх походження шляхом дивергенції під дією природного добору.
Питання лікування і профілактики спадкових хвороб не можна розв'язати без дослідження на тваринах із спадковими аномаліями, які подібні до тих, що спостерігаються у людини. Багато патологічних станів, що їх виявлено у тварин, можуть бути моделями спадкових хвороб людини. Так, у собак спостерігається гемофілія, яка зчеплена із статтю. Для вивчення м'язової дистрофії слугують миші, велика рогата худоба, коні, епілепсії — кролі, пацюки, миші. Спадкова глухота існує у гвінейських свинок, мишей і собак. Вади будови обличчя людини, гомологічні «заячій губі» та «вовчій пащі», спостерігаються в лицьовому відділі черепа мишей, собак, свиней. Спадковими хворобами обміну, такими як ожиріння і цукровий діабет, хворіють миші.
Отже, згідно із законом гомологічних рядів, вивчивши ряд форм у межах одного виду чи роду, можна передбачити наявність форм із подібними ознаками в межах близьких видів чи родів.